치즈 물성의 객관적 측정을 위한 고찰

Introduction

The primary quality factors of foods are texture, flavor, appearance, and nutrition. The term ‘textural properties’ can be defined as ‘group of physical characteristics that arise from the structural elements of the food, are sensed primarily by the feeling of touch, are related to the deformation, disintegration, and flow of the food under a force, and are objectively measured by functions of mass, time, and distance’ (Bourne, 2002). Rheological properties of cheese are critical to help us understand how the textural properties of cheese as a function of composition, cheese making conditions, such as acidification rate and extent, homogenization, and storage conditions (Lucey et al., 2003; Hassan et al., 2004). In this review, the objective measurement of rheological properties of cheese will be reviewed.

Rheological Properties of Foods

In food processing, understanding rheological properties is important for the following areas (Steffe, 1996; Velez-Ruiz and Barbosa Canovas, 1997):

Food rheology is defined as ‘the study of the deformation and flow of raw materials, intermediate products, and final products of the food industry’ (Bourne, 2002). Therefore, the concept of stress and strain is essential to understand rheolgy. Stress (σ) is defined as the force applied per unit area and is expressed in units of pascals (Pa).

$\sigma =F/A$

Where σ is the stress, F is a force, and A is area (Bourne, 2002).

There are two types of stress, which are normal stress and shear stress, depending on the direction of the force to the surface area. If the force perpendicularly acts to a sample surface, it is a normal stress. Chewing gum and kneading of dough can be examples of normal stress. On the other hand, if a parallel force is applied to a sample, it is called a shear stress. The spreading of butter over a toast and pumping of milk through pasteurizer are examples of shear stress.

Strain is defined as relative deformation when a stress is applied to a material and is a dimensionless quantity. An elastic material will deform with an application of shear stress while a viscous material will flow at a certain shear rate ($\stackrel{\cdot }{\gamma }$), which has a reciprocal second (s^-1)asunit (Rosenthal, 1999).

$\stackrel{\cdot }{\gamma }=dr/dt$

Where $\stackrel{\cdot }{\gamma }$ is the shear rate, t is the time (Rosenthal, 1999).

In physical terms, many food including cheese are considered as viscoelastic materials meaning that this material simultaneously exhibits some of the elastic properties of an ideal solid and some of the viscous properties of an ideal liquid (Bourne, 2002; Lucey et al., 2003). Differences between ideal elastic solid, an ideal liquid, and a viscoelastic material are shown in Fig. 1 where it is assumed a constant stress applied to materials and then the stress is released (Bourne, 2002).

Fig. 1. Schematic representation of elastic solid, Newtonian liquid, and viscoelastic solid (Bourne, 2002).

Download Original Figure

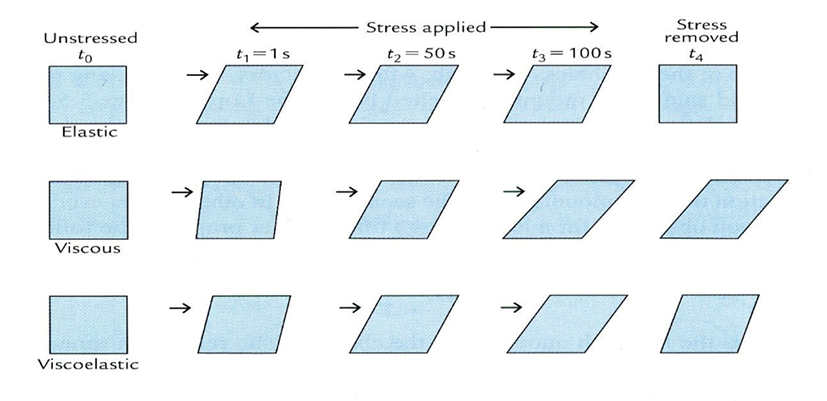
1) Elastic solid: when a force is applied to materials, an instantaneous deformation occurs. When the force is released, materials have a complete recovery of its original shape.

2) Newtonian liquid (ideal liquid): As soon as the force is applied, Newtonian liquid starts to flow. When the force is removed, Newtonian liquid will not recover to its original shape.

3) Viscoelastic solid: When force is applied, there is an instantaneous deformation. After the force is removed, viscoelastic solid will partly recover to the original shape but do not exhibit a full recovery.

Rheological Measurement of Cheese

The understanding of rheological properties of cheese is important since rheological properties of cheeses can affect texture and eating quality, physical properties, such as crumble and fracture, production of eyes and gas retention in cheeses (Roginski et al., 2003). To evaluate the rheological properties of cheese, several instrumental methods can be used. Instrumental methods can be grouped into three main categories, which are empirical, imitative and fundamental methods.

Empirical instrumental methods are used to assess variables, which are poorly defined, but can be related to qualities of texture from practical experience (Bourne, 2002). Penetration, compression, and cutting tests are included in these types of methods (Roginski et al., 2003). Although empirical instrumental methods may have problems regarding the poor definition of measured variables, these tests are the most widely used in food industry and provide a rapid, easy, and inexpensive way to determine rheological properties of foods (Bourne, 2002).

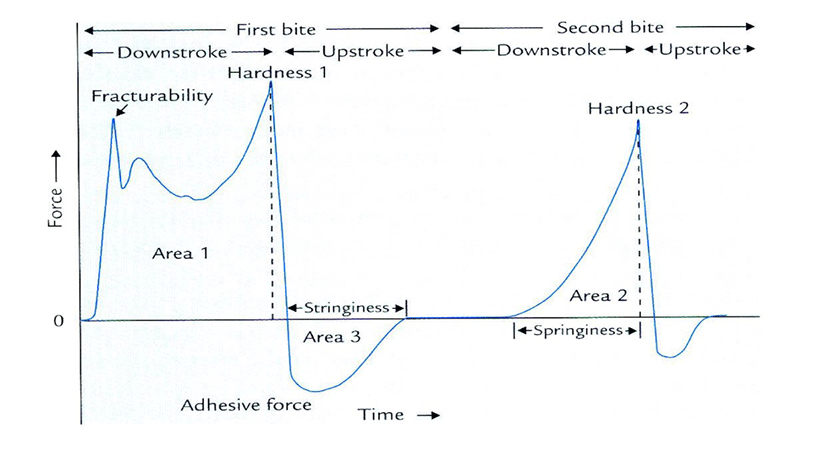
Imitative instrumental methods, which imitate mastication by a machine that “chews” the food, provide information regarding mastication or breakdown properties of cheese (Rosenthal, 1999). These methods may provide links between sensory breakdown (referred to as ‘chew down’) and instrumental results (Brown et al., 2003; Foegeding, 2003). Texture profile analysis (TPA) is one of these in imitative instrumental methods. A typical stress strain TPA curve with a two-bite cycle is illustrated in Fig. 2.

Fig. 2. A generalized texture profile analysis curve (Bourne, 2002).

Download Original Figure

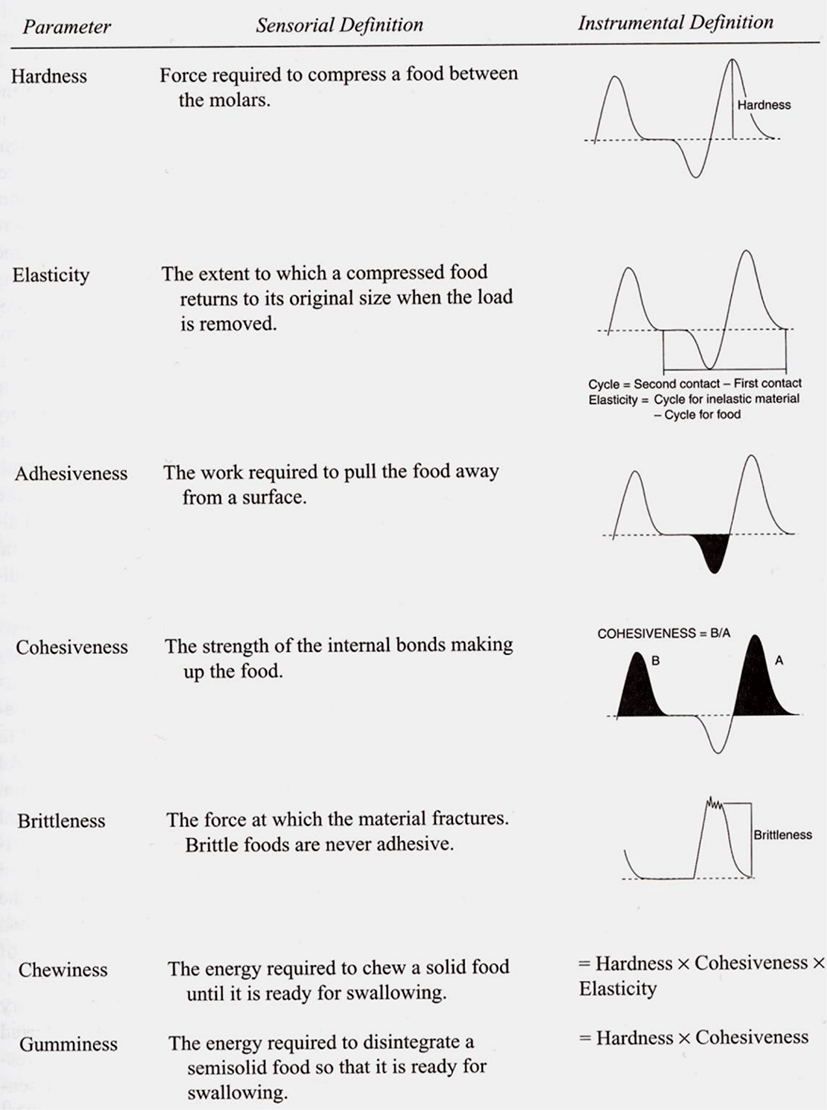
In TPA, a flat-ended plate, which compact food samples, deforms foods imitating the human jaw (Rosenthal, 1999). Since TPA tests attempt to imitate the human sensory perception of food texture, the first and second compression cycles imitate the first and second bite of mastication (Steffe, 1996). From the TPA curve shown in Fig. 2, several textural parameters, such as hardness, elasticity, adhesiveness, cohesiveness, brittleness, chewiness, and gumminess, can be determined and used to relate sensorial textural definitions with instrumental definitions (Fig. 3). It is clear that the development of TPA has proved to be a valuable method for the evaluation of food texture. However, it should be considered that the relationships between some of sensory properties, which TPA intends to evaluate, are not linear (Rosenthal, 1999).

Fig. 3. Textural parameters determined by Texture Profile Analysis (Rosenthal, 1999).

Download Original Figure

Well-defined rheological properties, such as Young’s modulus, are measured by fundamental instrumental methods (Rosenthal, 1999). Data obtained from fundamental tests are expressed in well-defined scientific units. Examples of fundamental instrumental techniques include dynamic low amplitude oscillatory shear rheometry and uniaxial compression (Gunasekaran and Ak, 2003).

Small Amplitude Oscillatory Rheology

Small amplitude oscillatory rheology (SAOR), also called dynamic rheological experiment, can be a powerful tool to determine the viscoelastic behavior of foods without damaging the network or structure, which requires the use of a small relative deformation (strain) (e.g. <5%).

In SAOR tests, a sinusoidal oscillatory stress or strain is applied to samples in the linear viscoelastic region where stress and strain are linearly related and responding strain or stress is measured (Steffe, 1996; Rao, 1999). Several rheological parameters can be determined in a SAOR test. Elastic or storage modulus (G′) is defined as the magnitude of energy stored per oscillation cycle and reflects the solid-like properties. Viscous or loss modulus (G″) is the measure of energy lost as viscous dissipation per cycle of deformation and indicates the liquid-like properties. Therefore, food materials will have more solid-like properties if G′ is greater than G″ while food materials will behave more like a liquid if G″ is greater than G′. It can be noted that for pure elastic solids, all the energy is stored meaning that G″ is zero while, for pure viscous fluids, all the energy is dissipated resulting in G′ that is zero (Rao, 1999).

For the characterization of viscoelastic materials as a function of time, a dynamic oscillatory test can be used. In controlled strain rheometry, the applied strain oscillates sinusoidally in time with an angular frequency while a sinusoidal stress function is subjected to the sample in controlled stress rheometry (Steffe, 1996; Van Vliet, 1999). In SAOR, a sinusoidal varying shear strain ($\gamma$) is subjected with an angular frequency (ω). Equation 3 gives the strain input function as a function of time.

$\gamma (t)={\gamma }_0\sin (\omega t)$

Where ${\gamma }_0$is the maximum shear strain, ω is the angular frequency, and t is time required to complete one cycle (van Vliet, 1999).

Equation 4 is generated by differentiation of equation 3.

$\stackrel{\cdot }{\gamma }(t)={\gamma }_0\omega \cos (\omega t)$

Where $\stackrel{\cdot }{\gamma }$ is the strain rate.

When food materials behave in a linear viscoelastic manner, sinusoidally varying shear stress is generated by the input of applied strain.

$\sigma (t)={\sigma }_0\sin (\omega t+\delta )$

Where σ₀ is the shear stress amplitude and δ is the phase angle.

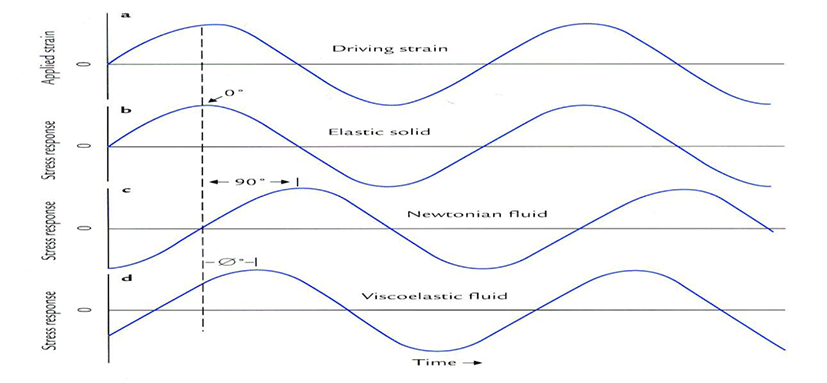
As described in equation 5, viscoelastic materials have the phase angle (δ), which is a measure of how much the stress and strain are out of phase with each other. The phase angle (δ) varies between 0 and π/2 radians as the viscous component increases. For an ideal elastic material, the stress is in phase with the strain meaning that the phase angle is 0° while the stress is ½ π radian or 90° out-of-phase with strain for an ideal viscous component, as illustrated in Fig. 4 (van Vliet, 1999; Rao, 1999).

Fig. 4. Stress responses of an elastic solid, a Newtonian fluid, and viscoelastic material as a function to time in dynamic SAOR tests (Bourne, 2002).

Download Original Figure

For deformation within the linear viscoelastic range, the shear stress response to a sinusoidal strain input in terms of G′ and G″ can be expressed as follows;

${\sigma }_0=G´{\gamma }_0\sin (\omega t)+G˝{\gamma }_0\cos (\omega t)$

G′ and G″ in terms of stress, strain, and phase angle can be derived from equations 4 and 6:

$G´=({\sigma }_0/{\gamma }_0)\cos \delta$

$G˝=({\sigma }_0/{\gamma }_0)sin\delta$

where G′ is the storage modulus, G″ is the loss modulus.

Loss tangent (tan δ) is the rheological parameter, which can be used to describe the viscoelastic behavior of food materials and is defined as ratio of loss modulus to storage modulus (G″/G′).

$\tan \delta =G˝/G´$

Loss tangent is related to the relative importance of the viscous component. If food material had a high loss tangent value (i.e., G″ > G′), a material has relatively more liquid-like properties and less solid-like properties (Rao, 1999).

Large Deformation and Fracture Rheology

Functional properties of rennet-induced gels, such as cutting, eating, and shaping characteristics, are associated with large deformation and fracture properties of gels (van Vliet and Walstra, 1995). Fracture may occur in food materials when all bonds making up the network break, which may lead to disintegration of the material (van Vliet Rosenthal, 1999). Large deformation tests can be performed by subjecting a low constant shear rate to the sample and this generates several rheological parameters, such as fracture stress (σ_fracture) and fracture strain ($\gamma$_fracture). σ_fracture and $\gamma$_fracture of gels are defined as the point when the shear stress starts to decrease (Lucey et al., 1997).

Conclusion

The objective measurement of textural and rheological properties of cheese has been reviewed. As has been explained, there are several methods that can be used to evaluate the rheological properties of cheese like textural profile analysis and small amplitude oscillatory rheological test. Which textural profile analysis is imitative instrumental method, deforms food imitating the human jaws which can easily quantify multiple textural parameters. Small amplitude oscillatory rheological test is fundamental method that can be used to determine the viscoelastic behavior of food behave more like a solid or liquid properties by measuring the value of G′ and G″.